在这里零散地记载一些遇到的密码学相关知识（当裁缝）

威尔逊定理

任一素数减去1的阶乘与-1模该素数同余。即对于任何素数p，都有
$$
(p-1)!+1\equiv 0(mod\ p)
$$

引理

设p是素数，f(x)是整系数多项式，再设a1,a2,…,an两两对模不同余，满足
$$
f(a_j)\equiv 0(mod\ p),1\leq j\leq n
$$
则存在整系数多项式q(x)，使得
$$
f(x)\equiv q(x)(x-a_1)(x-a_2)…(x-a_n)(mod\ p)
$$
由此可进一步推知，
$$
x^{p-1}-1\equiv (x-1)…(x-p+1)(mod\ p)
$$

群论

参考了百度百科和这篇文章

二元运算

image-20240306205145595

定义

image-20240306205505241

循环群

image-20240306210708812

阿贝尔群

若一个群满足交换律，则称其为阿贝尔群，也称为交换群。

同态

设(M,)和(S,·)是两个群，σ:M→S，∀a,b∈M，有σ(ab)=σ(a)·σ(b)，则称σ为M到S的同态或群映射。

也就是说，先运算再映射和先映射再运算得到的结果相等。

如果为单射，则称为单同态。

同构

如果一个同态映射可逆（双射），则称这两个群同构。

半群

只满足定义中的1、2两条

离散对数

当模m有原根时，设l为模m的一个原根，则当x=l^k mod m时，
$$
Ind_lx\equiv k(mod\ \phi(m))
$$
离散对数和一般的对数有着相类似的性质：
$$
Ind_lxy\equiv Ind_lx+Ind_ly(mod\ \phi(m))
$$

$$
Ind_lx^y\equiv yInd_lx(mod\ \phi(m))
$$

在程序中，我们可以用sympy库中的discrete_log函数来实现

1
2
3
4
5
import sympy
x=
y=
z=
e=sympy.discrete_log(x,y,z)  ##求e，discrete_log(x,y,z)，x为模，y为余数，z为底数

环和域

需要结合上面说到的群论来看，参考了这篇文章](https://blog.csdn.net/qq_51819011/article/details/129884474?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522170980296016800184186780%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=170980296016800184186780&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-1-129884474-null-null.142^v99^pc_search_result_base7&utm_term=%E7%8E%AF&spm=1018.2226.3001.4187)

定义

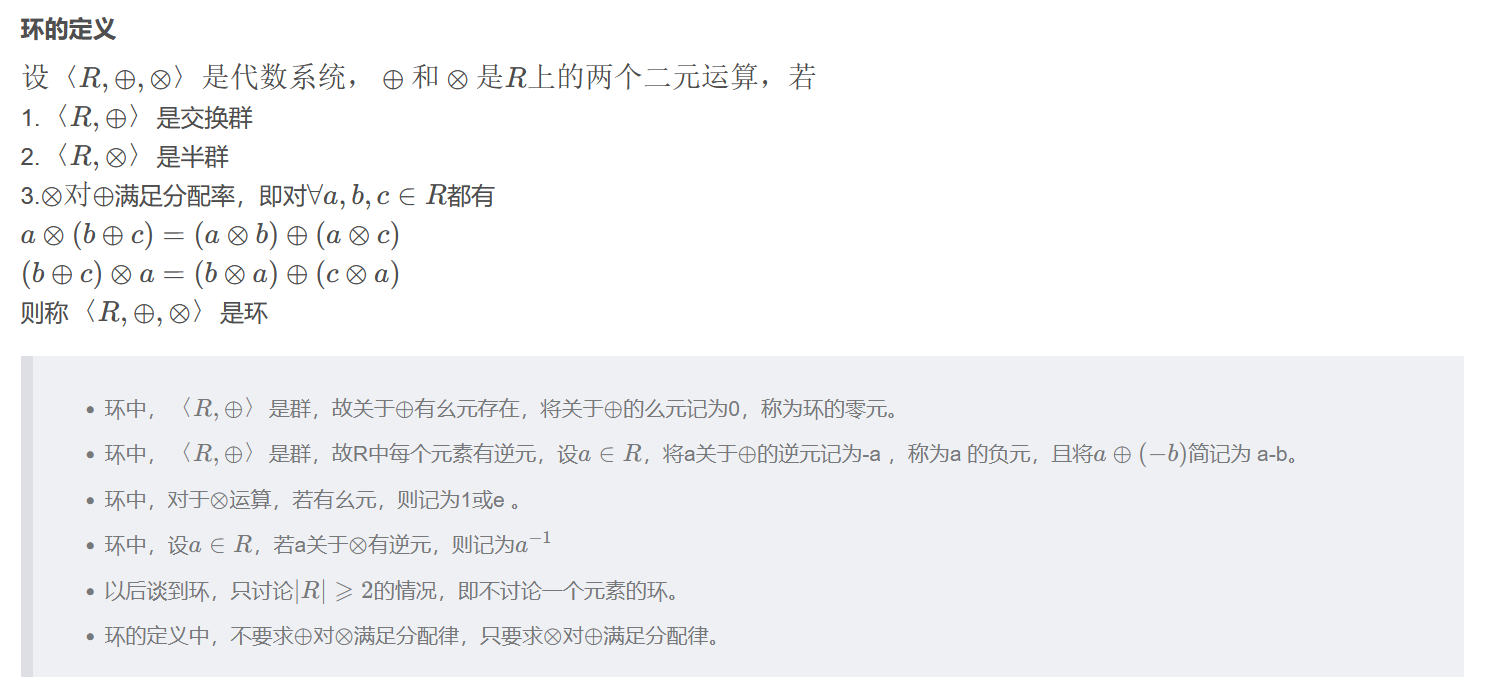
image-20240307204549987

交换环 含幺环 交换含幺环

image-20240307204829672

性质

image-20240307205000778

无零因子环和含零因子环

image-20240307205056700

image-20240307205356769

在有限含幺环中，无零因子等同于(非零元)有逆元。

整环（整区）

交换含幺的无零因子环称为整环。

除环

image-20240307205340140

除环是含幺的无零因子环。

域

接上面的环，参考了百度百科和这篇文章

定义

image-20240307205839086

可以说，可交换的除环是域，或有限整环是域

百度百科上的描述也不错

image-20240307211359034

有限域（伽罗瓦域）

如果域F只包含有限个元素，则称其为有限域。有限域中元素的个数称为有限域的阶。有限域的特征数必为某一素数p，因此它含的素域同构于Zp。若F是特征为p的有限域，则F中元素的个数为pⁿ,n为某一正整数。元素个数相同的有限域是同构的。因此，通常用GF(pⁿ)表示pⁿ元的有限域。GF(pⁿ)的乘法群是(pⁿ-1)阶的循环群。