浅学AI
简单学点AI,防止以后CTF中遇到AI就寄。。。
本文内容多为搬运+修补,所搬运文章链接在文末
朴素感知机、神经元
感知机接收多个输入信号,输出一个信号。感知机的信号只有“流 / 不流”(1/0)两种取值。这里我们认为 0 对应“不传递信号”, 1 对应“传递信号”。最简单的感知机就是将输入进行处理得到中间结果,再将结果经过非线性函数处理输出。一般的,我们也把上述的模型称为神经元 ,又称作节点(node)或单元(unit)。
神经网络
由多个神经元可组成神经网络。每个节点可以从其他节点接收输入,或者从外部源接收输入,然后计算输出。每个输入都各自的权重(weight,即 w),用于调节该输入对输出影响的大小,节点的结构如图所示:
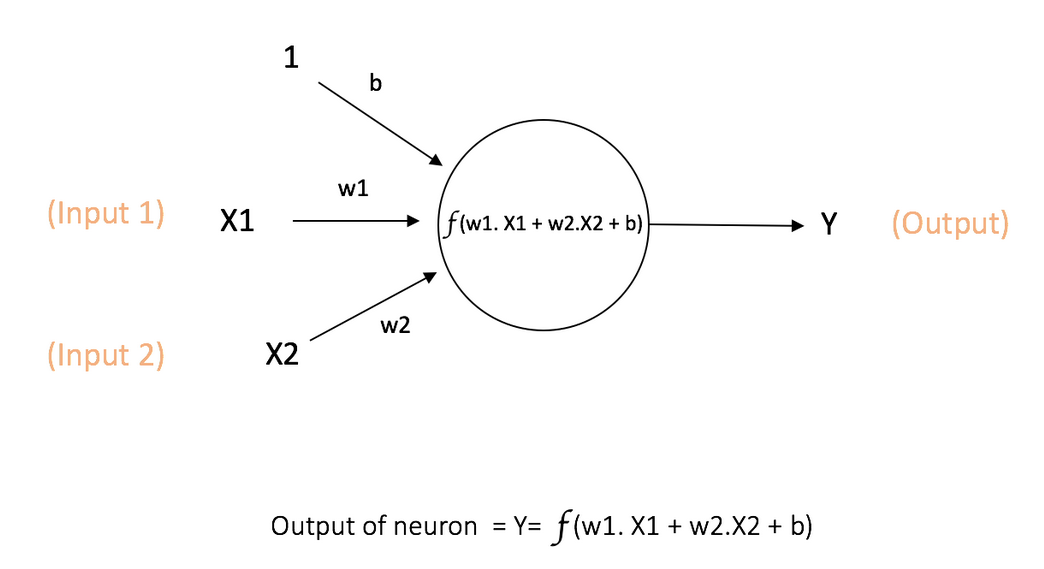
其中 x1, x2 作为该节点的输入,其权重分别为 w1 和 w2。同时,还有配有偏置b(bias)的输入 ,偏置的主要功能是为每一个节点提供可训练的常量值(在节点接收的正常输入以外)。
多层感知机
多层感知机(Multilayer Perceptron)缩写为 MLP,也称作前馈神经网络(Feedforward Neural Network)。它是一种基于神经网络的机器学习模型,通过多层非线性变换对输入数据进行高级别的抽象和分类。下图显示了一个最典型的 MLP,它包括包括三层: 输入层、隐层(全连接层)和输出层 (全连接的意思就是:上一层的任何一个神经元与下一层的所有神经元都有连接)。
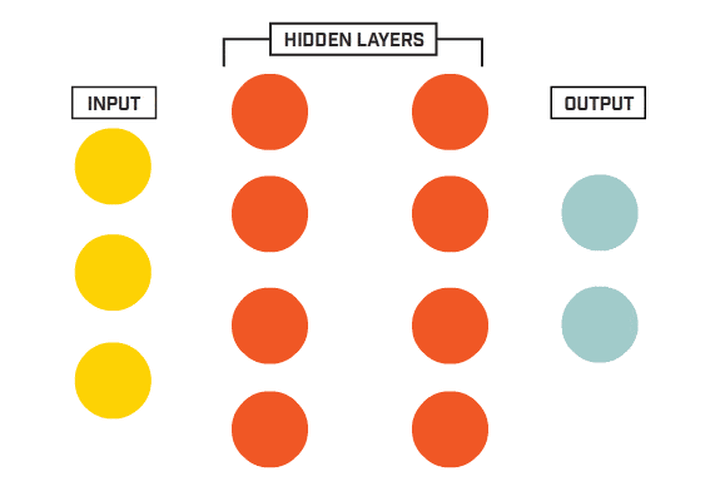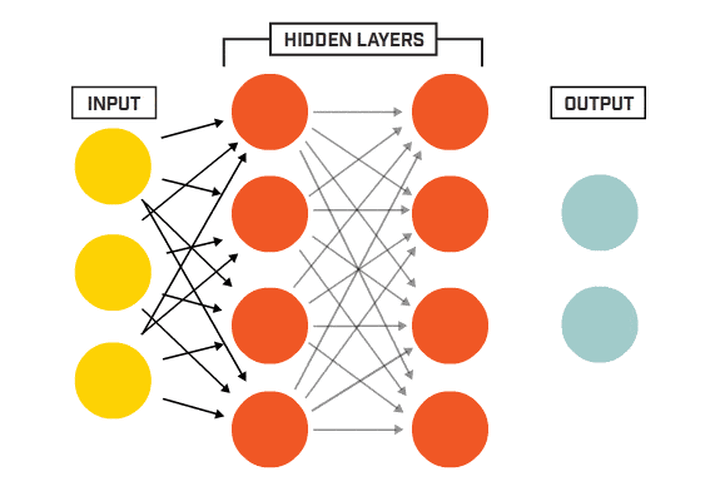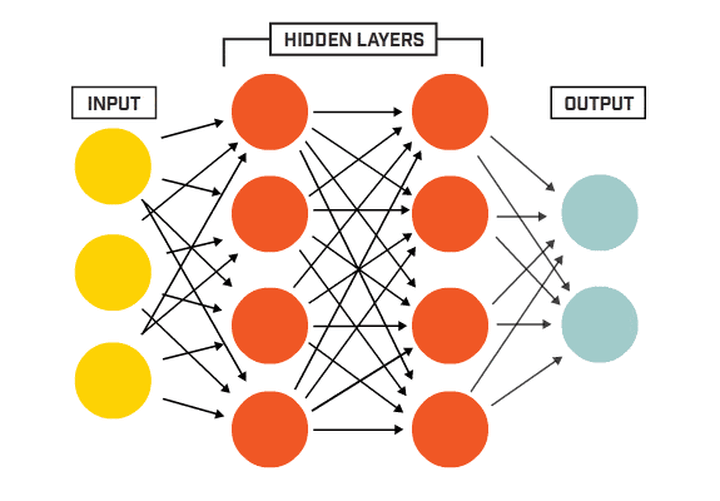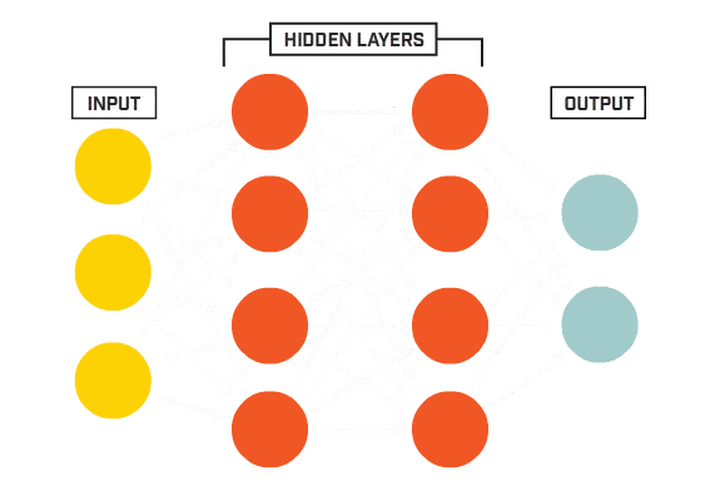
它的工作分为两部分:
- 前向传播 :输入数据被馈送到输入层,然后传递到隐藏层,并最终生成输出层的输出。每一层的每一个神经元都会计算其加权输入和非线性激活函数的输出。
- 反向传播 :在训练过程中,输出与期望的输出进行比较,产生一个误差值。这个误差随后被反向传播到网络中,权重得到相应的更新。
向前传播的计算
让我们把上面的 MLP 细节化:
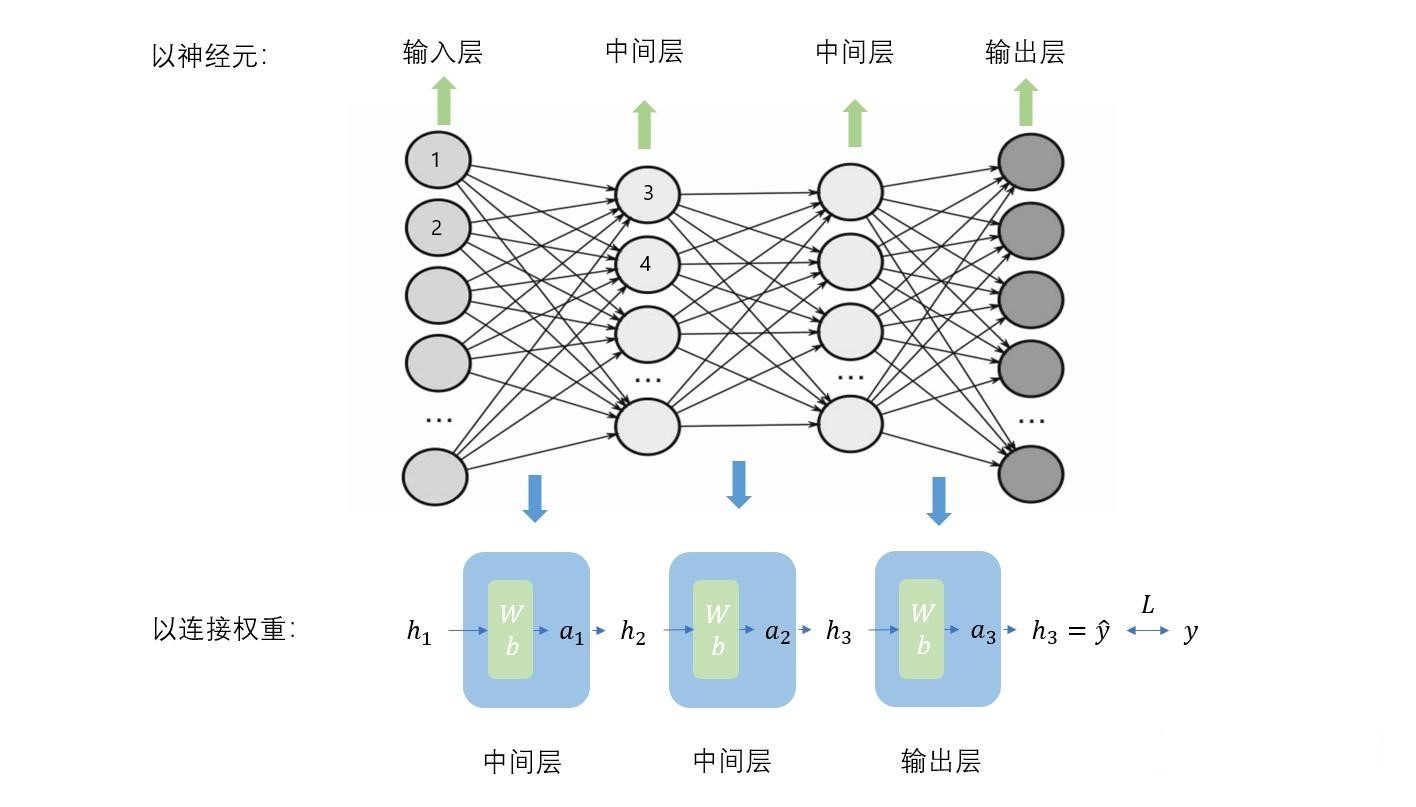
在一般情况下,参与运算的各元素都是 矩阵,其中的蓝色方块代表着 激活函数,绿色方块代表着 权重 Weight 和 偏置 Bias 。需要注意的是, *权重和偏置对应上图中不同神经元的连线*,例如 1-> 3 和 1-> 4 的参数不同。详细计算方式如下图及下式:
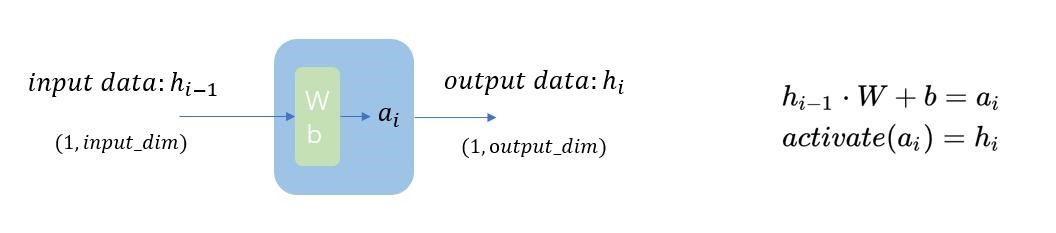
在分类问题中,最后的输出层元素个数一般等于分类数目,最终的结果代表着该输入被这个 MLP 分为某一类的可能性大小,指越大,代表越可能属于该类。为了便于观测,我们通常使用 softmax 函数将将上一层的原始数据进行归一化,转化为一个(0,1)(0,1) 之间的数值,这些数值可以被当做概率分布,用来作为多分类的目标预测值。
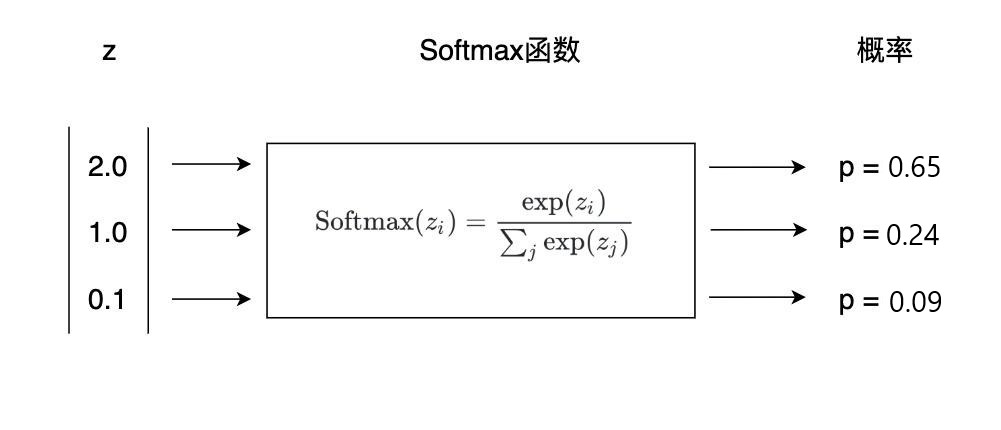
激活函数
激活函数可为神经元引入非线性因素,使神经网络能够处理更复杂的问题。如果没有激活函数,那么神经网络将变为由一个巨大的线性组合构成。
BP误差反向传播法
反向传播算法的核心概念是:通过比较现实输出与期望输出之间的差异,根据差异来反向更新每一层的参数,从而使现实输出更加贴近于期望输出。
损失对参数梯度的反向传播可以被这样直观解释:由 A 到传播 B,即由 ∂L/∂A∂L/∂A 得到 ∂L/∂B∂L/∂B ,由导数链式法则 ∂L/∂B=(∂L/∂A)⋅(∂A/∂B)∂L/∂B=(∂L/∂A)⋅(∂A/∂B)。所以神经网络的 BP 就是通过链式法则求出L对所有参数梯度的过程。
如下图示例,输入x,经过网络的参数 w,b ,得到一系列中间结果 a,h 。
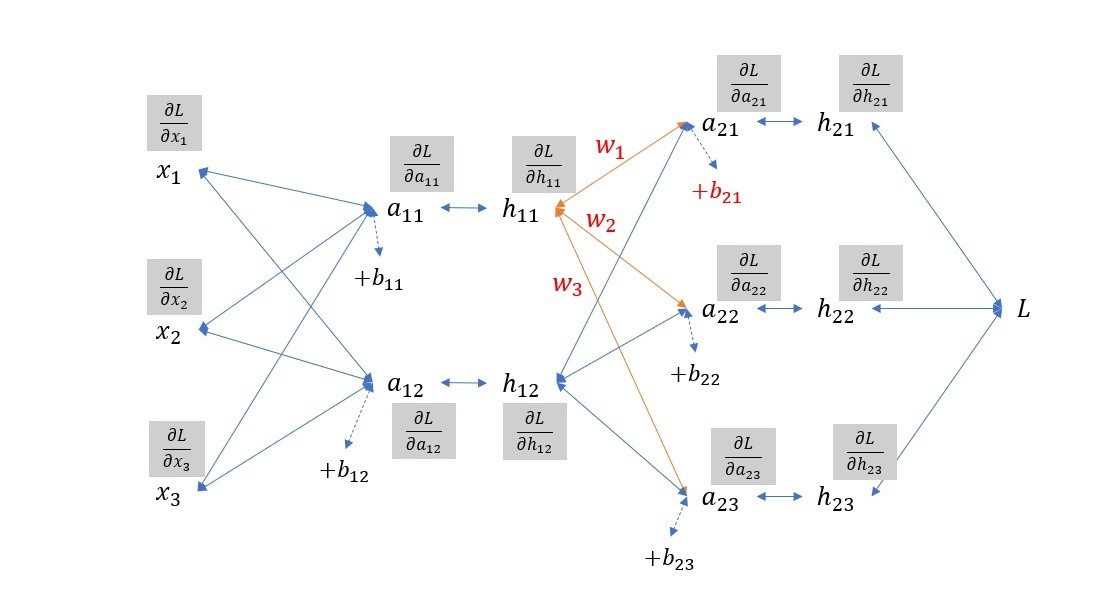
下面是具体的推导公式
右上角的h21到a21: \[ \frac{\partial l}{\partial a_{21}}=\frac{\partial l}{\partial h_{21}}*\frac{\partial h_{21}}{\partial a_{21}}=\frac{\partial l}{\partial h_{21}}*activate'(a_{21}) \] a21到h11: \[ L=f(a_{21},a_{22},a_{23})\frac{\partial L}{\partial h_{11}}=\frac{\partial L}{\partial a_{21}}\frac{\partial a_{21}}{\partial h_{11}}+\frac{\partial L}{\partial a_{22}}\frac{\partial a_{22}}{\partial h_{11}}+\frac{\partial L}{\partial a_{21}}\frac{\partial a_{21}}{\partial h_{11}}=\frac{\partial L}{\partial a_{21}}w_1+\frac{\partial L}{\partial a_{22}}w_2+\frac{\partial L}{\partial a_{23}}w_3 \]
\[ \frac{\partial L}{\partial w_1}=\frac{\partial L}{\partial a_{21}}\frac{\partial a_{21}}{\partial w_1}=\frac{\partial L}{\partial a_{21}}h_{11} \]
\[ \frac{\partial L}{\partial b_{21}}=\frac{\partial L}{\partial a_{21}}\frac{\partial a_{21}}{\partial b_{21}}=\frac{\partial L}{\partial a_{21}} \]
因此,我们可以如下图,将反向传播的表达式如下。

当然并不是所有的反向传播都是如此即可,还有可能与向前传播时所用的激活函数有关,具体可查看原文
参考文章:







