《初等数论》学习笔记
从今天开始,不间断地更新一些《初等数论》学习笔记,简单打一下密码学的基础
(为了密码学不爆零T0T)
第一章 整数的整除性
gcd(a,b)=gcd(b,r)
假设a和b都是整数,且a>b
a=bq+r, 0<r<b
其中q和r都是正整数,则a和b的最大公因数等于b和r的最大公因数,即
gcd(a,b) = gcd(b,r)
欧几里得算法(辗转相除法)
利用上述性质,我们可以用欧几里得算法来求两个较大数的最大公因数。用语言通俗地表达,就是先用较大数除以较小数,然后用上一个式子的除数除以上一个式子的余数,如此反复至余数为0,最后一个式子的除数即为最大公因数。
百度百科中的这张图较好地解释了其中原理:

下面是一个简单的python函数实现:
1 | def gcd(a, b): |
扩展欧几里得算法
看书上都没有讲,但是也很重要,这里补充一下。
这个算法在用辗转相除法找到gcd(a,b)的前提下,还能找到x,y,使得ax+by=gcd(a,b)。(根据贝祖/裴蜀定理,x和y总是存在)
具体原理引用这篇文章来讲https://blog.csdn.net/qq_37701948/article/details/132716594

如此可以得到欧几里得算法中前后两步之间x和y的关系,已知最后一步时b=0,于是可以以此倒推出原来的x和y,下面是一个简单的python函数实现:
1 | def ext_euclid(a, b): |
特别地,当a和b互素的时候,gcd(a,b)=1,因此要求的就是能使ax+by=1成立的x和y。这里的x其实就是a的模反元素(模逆元),在RSA解密中有着重要作用,以后的文章中再做详细的描述。
ab=dm
假设a和b都是正整数,a和b的最大公因数是d而a和b的最小公倍数是m,即(a,b)=d而{a,b}=m,则我们有
ab=dm
这可以用来更快捷地求出大数的最小公倍数:我们可以先试用欧几里得算法求出最大公因数,所以m=ab/d
第二章 数的进位法
求补码
对于二进制数(a1a2...an)2,当n≥3时,可用如下方法快速求补码
当an=1时
除an不变,在a1,a2,...an-1中所有ai是0的都变成1,而所有ai是1的都变成0。由这种方法所得到的二进制数就是(a1a2...an)2的补码
当an=0时
在(a1a2...an)2中从右往左看,则在出现1以前所有的0及其第一次出现的1都不变,而后各数遇0变成1,遇1则变成0.用这种方法所得到的二进制数就是(a1a2...an)2的补码。
利用补码来进行二进制数减法运算
先求减数的补码,用被减数加上补码再减去减数
第三章 一部分不定方程
一元不定方程
设n≥2,而n,a0,a1,...,an都是整数,求出关于整数系数的n次方程 \[ a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0=0 \] 设x=α是其整数解,那么 \[ a_n\alpha^n+a_{n-1}\alpha^{n-1}+...+a_1\alpha+a_0=0 \]
\[ a_0=-\alpha(a_n\alpha^{n-1}+a_{n-1}\alpha^{n-2}+...+a_1) \]
所以只要能从a0中挑选出能使原式成立的因数,即为原式的整数解,否则无整数解
二元一次不定方程
定理
设二元一次不定方程ax+by=c(其中a,b,c都是正整数而gcd(a,b)=1,有一组整数解x=x0,y=y0,则其一切整数解可以表示成 \[ \begin{cases} x=x_0-bt \\ y=y_0+at \end{cases} \] 其中t=0,±1,±2,±3,...
求ax+by=c的一切整数解
假设gcd(a,b)=1,
先求ax+by=1的解,可利用第一章中所述之扩展欧几里得算法,得到解x=x0,y=y0.
所以ax+by=c(ax0+by0),
所以x=cx0,y=cy0.
由上述定理得,x=cx0-bt,y=cy0+at,其中t=0,±1,±2,±3,...
如果放在实际应用问题中,要记得注意定义域。
费马大定理
当n是一个大于2的正整数时,则 \[ x^n+y^n=z^n \] 这个不定方程没有正整数解。
第四章 一次同余式及解法
同余
如果a和b都是整数而m是一个固定的正整数,则当m|(a-b)(即m能够整除a-b)时,我们就说a,b对模m同余,记作 \[ a\equiv b(mod\ m) \]
一些结论
1
当a是整数而m是一个正整数时,则有 \[ a\equiv a(mod\ m) \]
2
如果a,b都是整数而m是一个正整数,则当 \[ a\equiv b(mod\ m) \] 成立时,我们有 \[ b\equiv a(mod\ m) \]
3
如果a,b,c都是整数而m是一个正整数,则当 \[ a\equiv b(mod\ m) \]
\[ b\equiv c(mod\ m) \]
都成立时,我们有 \[ a\equiv c(mod\ m) \]
4
如果a,b,c,d都是整数,而m是一个正整数,则当 \[ a\equiv b(mod\ m) \]
\[ c\equiv d(mod\ m) \]
都成立时,我们有 \[ a+c\equiv b+d(mod\ m) \]
\[ a-c\equiv b-d(mod\ m) \]
5
如果a,b,c都是整数,而m是一个正整数,则当 \[ a\equiv b(mod\ m) \] 成立,我们有 \[ ac\equiv bc(mod\ m) \]
6
如果a,b,c,d都是整数,而m是一个正整数,则当 \[ a\equiv b(mod\ m) \]
\[ c\equiv d(mod\ m) \]
都成立时,我们有 \[ ac\equiv bd(mod\ m) \]
7
如果a,b都是整数,而m和n都是正整数,则当 \[ a\equiv b(mod m) \] 成立时,我们有 \[ a^n\equiv b^n(mod\ m) \]
8
如果a1,a2,...an,b1,b2,...bn都是整数,而m和n都是正整数,则当 \[ a_1\equiv b_1(mod\ m) \]
\[ a_2\equiv b_2(mod\ m) \]
...... \[ a_n\equiv b_n(mod\ m) \]
都成立时,我们有 \[ a_1+a_2+...+a_n\equiv b_1+b_2+...+b_n(mod\ m) \]
9
按照通常方法,把一个正整数a写成十进位数的形式,即 \[ a=a_n10^n+a_{n-1}10^{n-1}+...+a_0,0\leq a_i<10 \] 当9能够整除an+an-1+...+a0时,则我们有9能够整除a
弃九法
\[ a=a_n10^n+a_{n-1}10^{n-1}+...+a_0 \]
\[ b=b_m10^m+b_{m-1}10^{m-1}+...+b_0 \]
\[ ab=P \]
\[ P=c_l10^l+c_{l-1}10^{l-1}+...c_0 \]
由上面的结论,我们可以得到 \[ a\equiv a_n+a_{n-1}+...+a_0(mod\ 9) \]
\[ b\equiv b_n+b_{n-1}+...+b_0(mod\ 9) \]
\[ P\equiv c_n+c_{n-1}+...+c_0(mod\ 9) \]
进而得到 \[ (a_n+a_{n-1}+...+a_0)(b_m+b_{m-1}+...+b_0)\equiv c_l+c_{l-1}+...+c_0(mod\ 9) \] 如果an,an-1,...a0,bm,bm-1,...b0,cl,cl-1,...c0中有9出现,可以把9去掉
一次同余式
如果a,b都是整数,而m是一个正整数,当a mod m ≠0时,我们把 \[ ax+b\equiv 0(mod\ m) \] 叫做模m的一次同余式
一些结论
1
如果c能使ac+b mod m=0成立,则x mod m =c的一切整数x都能使其成立,也就是上式的一个解
2
当gcd(a.m)不能够整除b时,则一次同余式 \[ ax+b\equiv 0(mod\ m),a\ mod\ m\neq 0 \] 没有整数解
3
当gcd(a,m)=1时,则一次同余式 \[ ax+b\equiv 0(mod\ m),a\ mod\ m\neq 0 \] 有整数解
4
如果ad mod md =bd,则有a mod m=b


孙子定理(中国剩余定理)
如果k≥2,而m1,m2,...mk是两个两两互素的k个正整数,也就是说,在这k个正整数中任意取出两个正整数来,则这两个正整数是互素的,令 \[ M=m_1m_2...m_k=m_1M_1=m_2M_2=...=m_kM_k \] 则同时满足同余式组 \[ x\equiv b_1(mod\ m_1),x\equiv b_2(mod\ m_2),...,x\equiv b_k(mod\ m_k) \] 的正整数解是 \[ x\equiv b_1M'_1M_1+b_2M'_2M_2+...+b_kM'_kM_k(mod\ M) \] 这里M'i是满足同余式 \[ M'_iM_i\equiv 1(mod\ m_i) \] 的正整数解,i=1,2,...,k
其实百度百科上说的也不错:

根据不同的情况,中国剩余定理可以有不同的使用,但基本情况就是如上,对照着搓一下代码应该不难。
第五章 剩余系,欧拉定理,费马定理及其应用
完全剩余系

一些结论
1
设m是一个大于1的整数,b是一个整数且满足条件(b,m)=1.如果a1,a2,...am是模m的一个完全剩余系,则ba1,ba2,...,bam也是模m的一个完全剩余系
2
设m是一个大于1的整数,而b,c是两个任意的整数但满足条件(b,m)=1,如果a1,a2,...,am是模m的一个完全剩余系,则ba1+c,ba2+c,...,bam+c也是模m的一个完全剩余系
3
如果m是一个大于1的整数而a,b是任意的两个整数,使得 \[ a\equiv b(mod\ m) \] 成立,则有gcd(a,m)=gcd(b,m)
欧拉函数φ(m)
我们用φ(m)来表示不大于m而和m互素的正整数的个数。我们把φ(m)叫做欧拉函数。其中φ(1)=1
引理
设l是一个正整数,p是一个素数,则我们有 \[ \varphi(p^l)=p^{l-1}(p-1) \]
简化剩余系


一个结论
设m是一个大于1的整数,a是一个整数且满足条件gcd(a,m)=1.如果b1,b2,...bφ(m)是模m的一个简化剩余系,则 \[ ab_1,ab_2,...,ab_{\varphi (m)} \] 也是模m的一个简化剩余系
欧拉定理
设m是一个大于1的整数,a是一个素数且满足条件gcd(a,m)=1,则我们有 \[ a^{\varphi(m)}\equiv 1(mod\ m) \] 上式在RSA算法中有重要作用
费马小定理
对于欧拉定理有一种特殊情况,那就是当模m为素数是时,此时就可以得到费马小定理 \[ a^{p-1}\equiv 1(mod\ p) \] ## 第六章 小数、分数和实数
一些结论
1
设0<a<b,且gcd(a,b)=1.如果a/b能表示成纯循环小数,则我们有gcd(b,10)=1
2
设0<a<b,且gcd(a,b)=1.令h是一个最小的正整数,能使 \[ 10^h\equiv 1(mod\ b) \] 成立,则a/b能表示成纯循环小数0.a1...ah
3
设b是一个正整数且gcd(10,b)=1,令h是一个最小的正整数,能使 \[ 10^h\equiv 1(mod\ b) \] 成立,则有h|φ(b)
4
设a,b,b1都是正整数,a<b,gcd(a,b)=1,b1>1,gcd(b1,10)=1.b=2α5βb1,其中α,β都是非负整数但不同时为0.令h是一个最小的正整数且能使 \[ 10^h\equiv 1(mod\ b_1) \] 则当α≥β时我们有 \[ \frac{a}{b}=0.a_t...a_a\dot a_\alpha...\dot a_{\alpha+h} \] 而当α<β时我们有 \[ \frac{a}{b}=0.a_1...a_\beta \dot a_{\beta+1}...\dot a_{\beta+h} \]
第七章 连分数和数论分数
连分数

当1≤k≤n是一个整数时,我们把[a1,a2,...,ak]=pk/qk叫做(22)的第k个渐进分数。
一些结论
1
设n≥3和连分数[a1,a2,...an]的渐进分数是p1/q1,p2/q2,...,pn/qn,则在这些剪辑分数之间,下面的关系式成立 \[ p_1=a_1,q_1=1,p_2=a_1a_2+1,q_2=a_2 \] 而当3≤k≤n时,则有 \[ p_k=a_kp_{k-1}+p_{k-2},q_k=a_kq_{k-1}+q_{k-2} \]
2
如果连分数[a1,a2,...,an]的n个渐进分数是pk/qk(其中k=1,2,...,n),则当k≥2时我们有 \[ p_kq_{k-1}-p_{k-1}q_k=(-1)^k \] 而当k≥3时我们有 \[ p_kq_{k-2}-p_{k-2}q_k=(-1)^{k-1}a_k \]
3
每一个有理数都能够表示成为有限连分数
4
设[a1,a2,...,an...]是一个无限连分数,pk/qk(k=1,2,...)是它的第k个渐进分数,则当k≥2时我们有 \[ \frac{p_{2(k-1)}}{q_{2(k-1)}}>\frac{p_{2k}}{q_{2k}},\frac{p_{2k-1}}{q_{2k-1}}>\frac{p_{2k-3}}{q_{2k-3}},\frac{p_{2k}}{q_{2k}}>\frac{p_{2k-1}}{q_{2k-1}} \]
当k→∞时,pk/qk有一极限,则我们有 \[ \frac{p_1}{q_1}<\frac{p_3}{q_3}<\frac{p_5}{q_5}<...<[a_1,a_2,...,a_n...]<...<\frac{p_6}{q_6}<\frac{p_4}{q_4}<\frac{p_2}{q_2} \]
取整函数
设x是任何一个实数,我们用[x]来表示不大于x的最大整数,我们用{x}表示x-[x]
有如下性质:
x=[x]+{x},x-1<[x]≤x
当n是一个整数时,我们有[n+x]=n+[x]
当0≤x<1时,有[x]=0
循环连分数
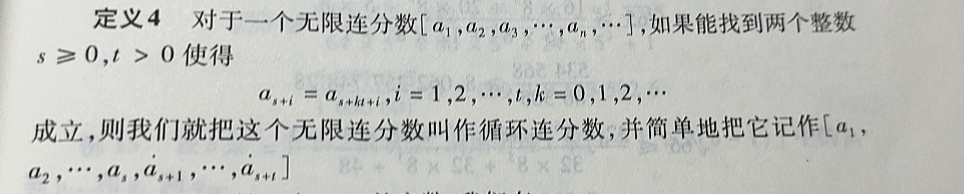
[x],{x}的一些性质
1
\[ [x]+[y]\leq [x+y],\{x\}+\{y\}\geq \{x+y\} \]
\[ [-x]=\begin{cases} -[x]+1, 当x不是整数时 \\ -[x], 当x是整数时 \end{cases} \]
2
设n是任一个正整数而α是一个实数时,则有 \[ [\alpha]+[\alpha+\frac{1}{n}]+...+[\alpha+\frac{n-1}{n}]=[n\alpha] \] 成立
3
设a,b是两个整数,b>0,则有 \[ a=b[\frac{a}{b}]+b\{\frac{a}{b}\},0\leq b\{\frac{a}{b}\}\leq b-1 \]
4
我们有 \[ [2x]+[2y]\geq [x]+[y]+[x+y] \]
一些数论函数
除了前面提到过的欧拉函数和取整函数以外,我们还有一些数论函数
除数函数
如果n是一个正整数,我们用d(n)来表示n的因数的个数。我们把d(n)叫做除数函数。
1
设n=p1α1...pmαm,其中p1,...pm都是不同的素数,而α1,...,αm都是正整数,则我们有 \[ d(n)=(\alpha_1+1)...(\alpha_m+1) \]
2
设a,b是两个正整数而gcd(a,b)=1,则我们有 \[ d(ab)=d(a)d(b) \]
因数和
如果n是一个正整数,则我们把n的所有因数相加以后所得到的和叫做n的因数和,记作σ(n)
1
设m,n是两个正整数且gcd(m,n)=1,则我们有 \[ \sigma (mn)=\sigma(m)\cdot\sigma(n) \]
真因数
如果n是一个正整数,则我们把除去n本身以外的n的因数都叫作n的真因数
完全数
如果n是一个正整数,当我们把n的所有真因数相加以后,所得到的和恰好等于n时,则我们把n叫作完全数。或者说当σ(n)=2n成立时,则我们把n叫作完全数。
1
如果n是一个≥2的整数而2^n-1是一个素数,则 \[ 2^{n-1}(2^n-1) \] 是一个完全数
σ和d的联系
如果n是一个正整数而λ是一个非负整数,则令 \[ \sigma_\lambda(n)=\sum_{d|n}d^\lambda \] 设m是一个整数,令m^0=1,我们有 \[ \sigma_0(n)=d(n) \] 另外 \[ \sigma_1(n)=\sigma(n) \]
莫比乌斯函数
\[ \mu(n)=\begin{cases} 1,当n=1时 \\ (-1)^r,当n是r个不同的素数的乘积时 \\ 0,当n能被一个素数的平方除尽时\end{cases} \]
1
如果m,n是两个正整数而gcd(m,n)=1,则我们有 \[ \mu(mn)=\mu(m)\cdot\mu(n) \]
2
我们有 \[ \sum_{d|n}\mu(d)=\begin{cases} 1,当n=1时 \\ 0,当n>1时\end{cases} \]
3
设n=p1α1...pmαm,其中p1,...pm是m个不同的素数,而α1,...,αm都是正整数,则我们有 \[ \sum_{d|n}|\mu(d)|=2^m \]
第八章 关于复数和三角和的概念
三角函数泰勒公式
这里贴一下三角函数泰勒公式

欧拉公式
\[ e^{i\theta}=cos\theta+isin\theta \]
并且由此可以推知, \[ |e^{i\theta}|=\sqrt{cos^2\theta+sin^2\theta}=1 \]
负数的指数式
根据上面的欧拉公式,复数z=r(cosθ+isinθ)可以表示为简单形式 \[ z=re^{i\theta} \]
一些结论
1
设θ1和θ2是两个实数,则我们有 \[ e^{i(\theta_1+\theta_2)}=e^{i\theta_1}\cdot e^{i\theta_2} \]
2
设n是一个正整数而z=a+bi是一个复数,则当z≠1时我们有 \[ \sum_{m=0}^n{z^m}=\frac{1-z^{n+1}}{1-z} \]
3
我们有 \[ \sum_{m=0}^{n-1}{e^{i(\theta+\frac{n-1}{2}\varphi)}}\cdot\frac{sin\frac{n\varphi}{2}}{sin\frac{\varphi}{2}} \] 其中n是一个正整数,φ≠2lπ,其中l是任一个整数,即{φ/2x}≠0
(也许暂时的)结尾
以上是本人读了前两册《初等数论》后记录的笔记。第二册的三角和部分及最后一册暂且先不读了,以后有需要再读了做补充。








