密码学算法散记
在这里零散地记载一些密码学可能用到的算法脚本
(当裁缝),方便之后直接拿来用
RSA中的e,phi不互素问题
参考了这篇文章
换模
当e和p-1或q-1互素时,可以转换到模p或模q下求解
假设e与p-1互素 \[ m^e\equiv c(mod\ n) \]
\[ m^e=c+kpq \]
\[ m^e\ mod\ p=c\ mod\ p+kpq\ mod\ p \]
\[ m^e\equiv c(mod\ p) \]
python实现:
1 | import gmpy2 |
e//gcd iroot(m,2)
当gcd(e,phi)较小时,可以先将e//gcd(e,phi),使得e和phi互素后,再对算出的m开根
python实现:
1 | import gmpy2 |
有限域内开方
有时,当e较小时,我们仍然无法用上面的方法得到m。这时,我们可以使用有限域内开方的方法。
前面我们已经证明了,当p为素数时,由 \[ m^e\equiv c(mod\ n) \] 可以推知 \[ m^e\equiv c(mod\ p) \] 于是我们可以设法找到所有满足 \[ m^e\equiv x^e\equiv c(mod\ p) \] 的x,以及所有满足 \[ m^e\equiv y^e\equiv c(mod\ q) \] 的y,从而列出 \[ \begin{cases}m\equiv x(mod\ p) \\ m\equiv y(mod\ q)\end{cases} \] 的方程组,通过中国剩余定理(CRT)求解。
下面是一个利用sagemath的程序实现
1 | from Crypto.Util.number import * |
当然也可以通过观察对算法进行一定的优化,详见上面给出的文章,这里不再赘述。
AMM算法
参考了这篇文章
当e比较大的时候,我们可以使用AMM算法,它能够大大提高运算的速度
原算法
先说明一下AMM算法的原算法,此时e=2,p为奇素数,对于 \[ x^2\equiv r(mod\ p) \] 我们先对两边开根 \[ x\equiv r^{\frac{1}{2}}(mod\ p) \] 令p-1=2^{s}t,又由欧拉定理得, \[ r^{\frac{p-1}{2}}\equiv r^{2^{s-1}t}\equiv 1(mod\ p) \]
当s=1时,
\[ r^t\equiv 1(mod\ p) \]
两边同时乘r,再开根,即推出公式 \[ r^{\frac{t+1}{2}}\equiv \pm \sqrt r\equiv \pm x(mod\ p) \] 将m和c代进去,就是这样(t可以根据p算出来) \[ \pm m\equiv c^{\frac{t+1}{2}} \]
当s>1时,
如果直接开根我们会得到一正一负两个式子 \[ r^{2^{s-2}t}\equiv 1(mod\ p) \]
\[ r^{2^{s-2}t}\equiv -1(mod\ p) \]
由上面得到的 \[ r^{2^{s-1}t}\equiv 1(mod\ p) \] 两边同时乘上这个式子,并用k来控制是否要乘(k=0,1) \[ r^{2^{s-2}t}n^{2^{s-1}tk}\equiv 1(mod\ p) \] 就这样反复对两边进行开方操作,直至回到前面s=1的情况,即 \[ r^tn^{t*(2k_1+2^2k_2+...+2^{s-1}k_{s-1})}\equiv 1(mod\ p) \] 两边乘上r再开方 \[ r^{\frac{t+1}{2}}n^{t*(k_1+2k_2+...+2^{s-2}k_{s-1})}\equiv\pm \sqrt r\equiv \pm x(mod\ p) \] 将m和c代进去,得到 \[ c^{\frac{t+1}{2}}n^{t*(k_1+2k_2+...+2^{s-2}k_{s-1})}\equiv \pm m(mod\ p) \]
e>2
对于 \[ x^e\equiv r(mod\ p) \] 令p-1=e^{s}t,则有 \[ r^{\frac{p-1}{e}}\equiv r^{e^{s-1}t}\equiv 1(mod\ p) \] 此时可以找到δ,使得t|(eδ-1),则 \[ r^{e^{s-1}(eδ-1)}\equiv 1(mod\ p) \]
当s=1时,
\[ r^{(eδ-1)}\equiv 1(mod\ p) \]
两边乘r,再开e次方 \[ r^\delta\equiv r^{\frac{1}{e}}\equiv x(mod\ p) \]
当s>1时,
构造e次非剩余集合 \[ K_i=\rho^{i*\frac{p-1}{e}}=\rho^{i*e^{s-1}t},0\leq i\leq e-1 \]
\[ K_i^e=\rho^{i*e^st}=\rho^{i*(p-1)} \]
所以根据欧拉定理,得 \[ \rho^{i*(p-1)}\equiv \rho^{(p-1)}\equiv1(mod\ p) \] 由上面的式子又可以推知 \[ \begin{cases}K_i=\rho^{\frac{i*(p-1)}{e}} \\ K_{e-i}=\rho^{\frac{(e-i)*(p-1)}{e}}\end{cases} \]
\[ K_i*K_{e-i}=\rho^{p-1} \] 由欧拉定理又可以得到 \[ K_i*K_{e-i}\equiv 1(mod\ p) \] 所以K_i和K_{e-i}互为逆元
对于前面这个式子 \[ r^{e^{s-1}(eδ-1)}\equiv 1(mod\ p) \] 两边开e次方得到一个集合K中的数设为K_{e-j} \[ r^{e^{s-2}(eδ-1)}\equiv K_{e-j}(mod\ p) \] 两边乘上K_j然后开e次方 \[ r^{e^{s-2}(eδ-1)}K_j\equiv K_{e-j}K_j\equiv 1(mod\ p) \]
\[ r^{e^{s-2}(eδ-1)}\rho^{j*e^{s-1}t}\equiv 1(mod\ p) \]
反复进行上述操作,直至回到s=1的情况 \[ r^{(eδ-1)}\rho^{ej_1+e^2j_2+...+e^{s-1}j_{s-1}}\equiv 1(mod\ p) \] 两边乘r,开e次方 \[ r^δ\rho^{j_1+ej_2+...+e^{s-2}j_{s-1}}\equiv r^{\frac{1}{e}}\equiv x(mod\ p) \] 将m和c代进去,得到 \[ c^δ\rho^{j_1+ej_2+...+e^{s-2}j_{s-1}}\equiv m(mod\ p) \] 此时我们便得到了其中一个根,剩余的根可以通过不断乘上集合K得到.
当我们得到了所有的解以后,使用中国剩余定理对下面的方程组求解即可 \[ \begin{cases} m^e\equiv cp(mod\ p) \\ m^e\equiv cq(mod\ q)\end{cases} \] python代码实现:
1 | import random |
当然,这里还得介绍一下sagemath中有一个很好用的方法.nth_root,可以非常有效地完成域下的高次开根
大概用法如下,可视情况做出修改
1 | K=Zmod(n) |
这样可以返回所有在模n整数环下,满足x^e ≡ c (mod n)的x
共模攻击
用于解决在GF(n)下,明文相同,公钥不同,而模n又很大难以分解的情况(两组公钥和密文已知) \[ \begin{cases}m^{e_1}\equiv c_1(mod\ n) \\ m^{e_2}\equiv c_2(mod\ n)\end{cases} \] 两边分别同时乘s1,s2次方 \[ \begin{cases}m^{e_1s_1}\equiv c_1^{s_1}(mod\ n) \\ m^{e_2s_2}\equiv c_2^{s_2}(mod\ n)\end{cases} \] 两式相乘 \[ m^{e_1s_1+e_2s_2}\equiv c_1^{s_1}c_2^{s_2}(mod\ n) \] 这里使用扩展欧几里得算法,我们可以找到能满足e1s1+e2s2=1的s1和s2。又因为一般来说m<n,所以 \[ m=c_1^{s_1}c_2^{s_2}\ mod\ n \] 代码实现:
1 | import gmpy2 |
维纳攻击
参考这篇文章
用于RSA中e很大的时候
代码实现:
1 | import gmpy2 |
Boneh Durfee攻击
类似维纳攻击,但可使d范围更大
1 | import time |
CBC字节翻转攻击
参考这篇文章
用于CBC模式下的AES加密
个人认为上面的文章中这一段讲得已经很清楚了
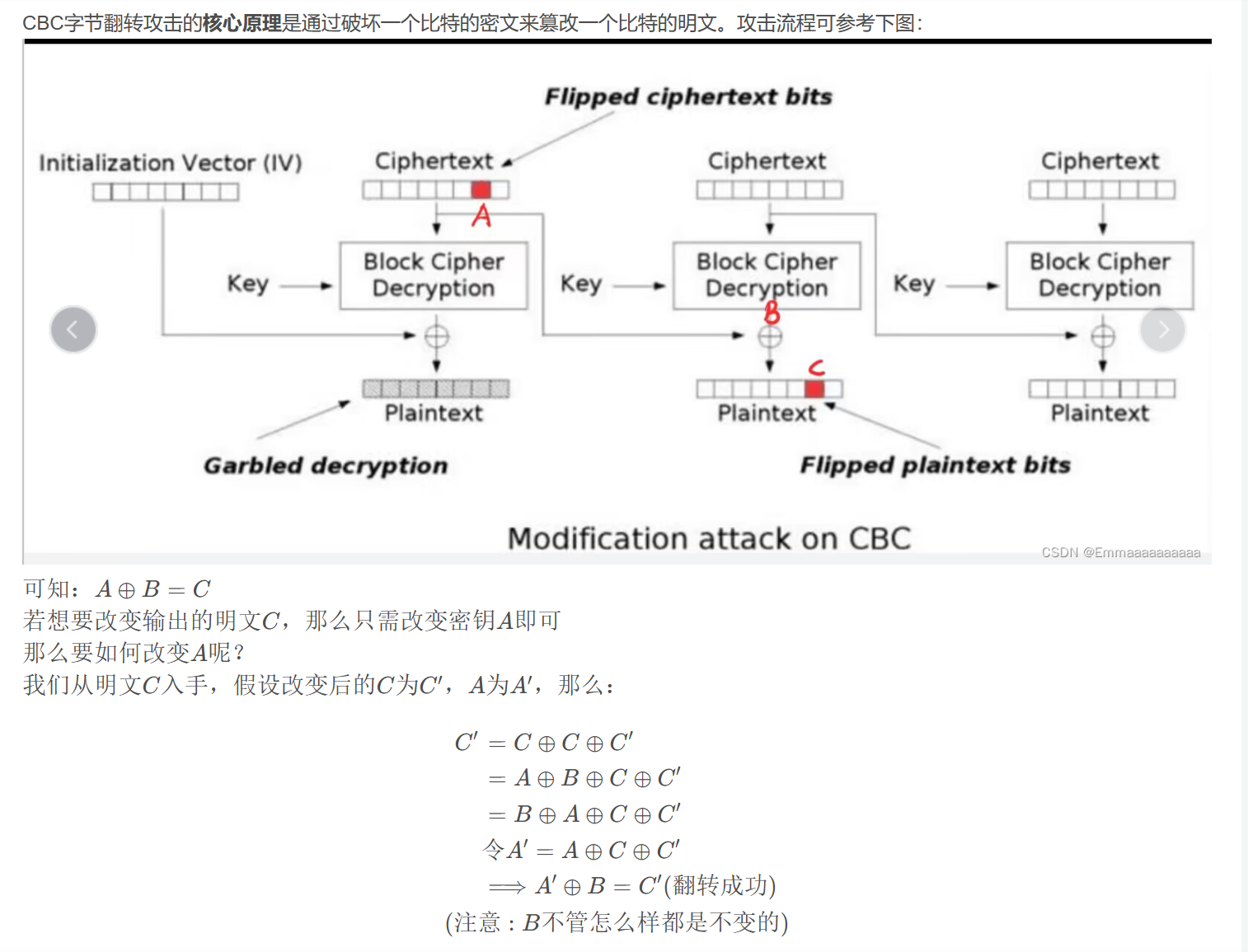
实现代码:
1 | def strxor(a1, a2): |
MT19937伪随机数预测
MT19937,即梅森旋转算法,是一种伪随机数的生成算法,python中的random模块生成“随机数”时使用的就是这种算法。
根据其原理,有一个叫randcrack的python模块可以对其生成的“随机数”进行预测,前提是需要已知已经生成的至少624个32位二进制数,这样才能预测出下一个生成的数会是多少。
实现代码:
1 | from randcrack import RandCrack |
那么前面给出的是312个64位数呢?
其实,random生成64位数的方式就是先生成2个32位数,然后将它们拼起来得到的。因此我们只需要把这个64位数拆开成两个32位数即可。
实现代码:
1 | from randcrack import RandCrack |
LCG
LCG,线性同余法,是一种生成伪随机数的方法,用一个公式来概括就是 \[ X_{n+1}=(aX_n+b)\ mod\ m \] 基本围绕以下四个公式,即可解决各类基础的LCG问题








